Depth First Search

Depth First Search is one of the main graph algorithms.

Depth First Search finds the lexicographical first path in the graph from a source vertex u to each vertex.

Depth First Search will also find the shortest paths in a tree (because there only exists one simple path), but on general graphs this is not the case.

The algorithm works in $O(m+n)$ time where n is the number of vertices and m is the number of edges.

Description

The idea behind DFS is to go as deep into the graph as possible, and backtrack once you are at a vertex without any unvisited adjacent vertices.

It is very easy to describe / implement the algorithm recursively:

We start the search at one vertex.
After visiting a vertex, we further perform a DFS for each adjacent vertex that we haven’t visited before.
This way we visit all vertices that are reachable from the starting vertex.

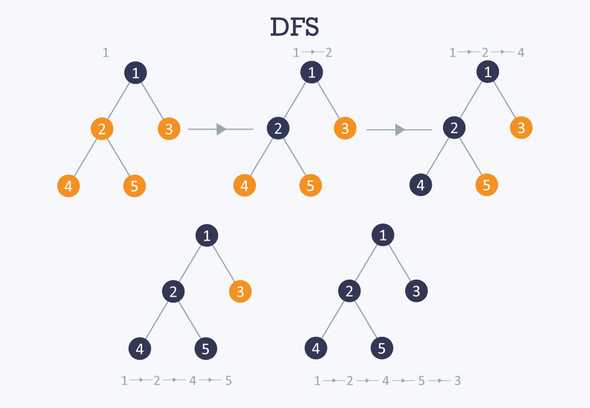
Example

Implementation

C++

#include <bits/stdc++.h>
using namespace std;

const int maxN = 1000001;

vector<int> G[maxN];
bool visited[maxN];

void dfs(int u) {
    visited[u] = true;
    cout << u << " ";
    for (int child: G[u]) {
        if (!visited[child])
            dfs(child);
    }
}


int main() {
    int vertices, edges;
    cin >> vertices >> edges;

    for (int i = 0; i < edges; i++) {
        int a, b;
        cin >> a >> b;

        // Since it is an undirected graph, so we will update adjacency list of both nodes
        G[a].push_back(b);
        G[b].push_back(a);

    }

    cout << "DFS Traversal: ";
    dfs(1); // We will start the traversal from 1st node since the graph is 1-based
    cout << endl;
    return 0;
}


// Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.

// Space Complexity: O(V). Since, an extra visited array is needed of size V.

Java

import java.util.*;

public class DFS {

	static class Vertex {
		public int id;
		public List<Vertex> edges;

		public Vertex(int id) {
			this.id = id;
		}
	}

	public static void dfs(int node, boolean[] visited, Vertex[] graph) {

		visited[node] = true;

		System.out.print(node + " ");

		for (Vertex child : graph[node].edges) {
			if (!visited[child.id])
				dfs(child.id, visited, graph);
		}
	}

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int vertices = sc.nextInt();
		int edges = sc.nextInt();

		Vertex[] graph = new Vertex[vertices + 1];
		boolean[] visited = new boolean[vertices + 1];

		for (int i = 1; i <= vertices; i++) {
			graph[i] = new Vertex(i);
			graph[i].edges = new ArrayList<Vertex>();
		}

		Vertex v1, v2;

		for (int i = 1; i <= edges; i++) {
			int a = sc.nextInt();
			int b = sc.nextInt();

			v1 = new Vertex(a);
			v2 = new Vertex(b);

			// Since it is an undirected graph, so we will update adjacency list of both nodes
			graph[a].edges.add(v2);
			graph[b].edges.add(v1);
		}

		System.out.println();
		System.out.print("DFS Traversal: ");

		// We will start the traversal from 1st node since the graph is 1-based
		dfs(1, visited, graph);

		System.out.println();

		sc.close();
	}
}

// Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
// Space Complexity: O(V). Since, an extra visited array is needed of size V.

Python

maxN = 1000001

G = {}
visited = [False] * maxN

# Initializing the adjacency list
for i in range(maxN):
    G[i] = list()

def dfs(u):
    visited[u] = True
    print(u, end=' ')
    for node in G[u]:
        if visited[node] is False:
            dfs(node)

vertices, edges = map(int, input().split())

for i in range(edges):
    a, b = map(int, input().split())

    # Since it is an undirected graph, so we will update adjacency list of both nodes
    G[a].append(b)
    G[b].append(a)

print("DFS Traversal: ")
dfs(1)  # We will start the traversal from 1st node since the graph is 1-based
print()

# Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
# Space Complexity: O(V). Since, an extra visited array is needed of size V.