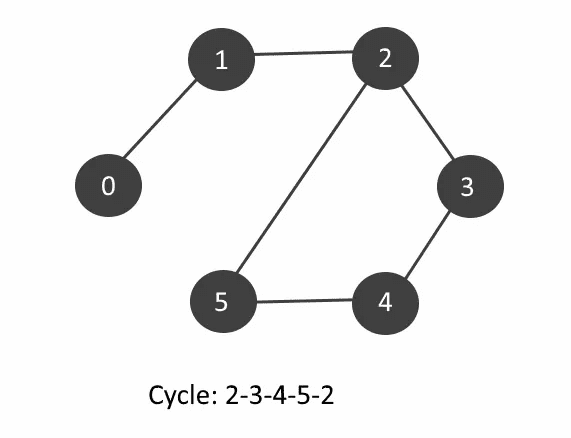
A undirected graph is said to be cyclic if there exists atleast one cycle among the vertices in the graph. If cycles are found, print all the cycles.
Description
- We will use the concept of Graph Coloring and color all the vertices which occur in a cyclic graph.
- We will run a series of DFS in the graph.
- Initially all vertices are colored WHITE (i.e white color can be represented by 0).
- From each unvisited white vertex, start the DFS, mark it GRAY (i.e gray color can be represented by 1) while entering and mark it BLACK (i.e black color can be represented by 2) on exit.
- If DFS moves to a gray vertex, then we have found a cycle.
- If a partially visited vertex (gray colored vertex) is found, backtrack till the vertex is reached again and mark all vertices in the path with a counter which is cycle number.
- After completion of DFS, we will iterate for cyclic edge and push them into a separate adjacency list.
- Print all the cycles number wise from the adjacency list.
Example
Implementation
C++
#include <bits/stdc++.h>
using namespace std;
const int maxN = 1000001;
vector<int> G[maxN];
// Stores the processing status of a vertex
int color[maxN];
// Stores the parent of a vertex
int parent[maxN];
// Stores the visited status of a vertex
int visited[maxN];
// Total number of cycles in the graph
int cycleNumber = 0;
void dfs(int u, int par = 0) {
// Idea is to mark a vertex by processing status
// 1. color = 0 -> If the vertex is not visited (white)
// 2. color = 1 -> To visit a vertex partially (gray)
// 3. color = 2 -> To visit a vertex completely (black)
// Already visited vertex.
if (color[u] == 2)
return;
// Cycle detected when a vertex is visited partially
if (color[u] == 1) {
cycleNumber++;
// Backtracking based on parents to find the complete cycle
int current = par;
visited[current] = cycleNumber;
while (current != u) {
current = parent[current];
visited[current] = cycleNumber;
}
return;
}
// Marking the parent of a vertex
parent[u] = par;
// Marking the node as partially visited
color[u] = 1;
// Running DFS on graph
for (int node : G[u]) {
// If the vertex is previously visited
if (node == parent[u])
continue;
// If the vertex is not visited
dfs(node, u);
}
// Marking the vertex as completely visited
color[u] = 2;
}
int main() {
int vertices, edges;
cin >> vertices >> edges;
for (int i = 0; i < edges; i++) {
int a, b;
cin >> a >> b;
// Since it is an undirected graph, so we will update adjacency list of both nodes
G[a].push_back(b);
G[b].push_back(a);
}
// Traversing from first node
dfs(1);
// Adjacency list to store the cycles
map<int, vector<int>> cycles;
for (int i = 1; i <= vertices; ++i)
{
if (visited[i] != 0) {
cycles[visited[i]].push_back(i);
}
}
// Printing the cycle
for (auto cycle : cycles) {
cout << "Cycle Number " << cycle.first << ": ";
for (int x : cycle.second)
cout << x << " ";
cout << endl;
}
return 0;
}Java
import java.util.*;
public class PrintCycle {
// Total number of cycles in the graph
public static int cycleNumber = 0;
static class Vertex {
public int id;
public List<Vertex> edges;
public Vertex(int id) {
this.id = id;
}
}
public static void dfs(int node, int[] visited, int[] color, Vertex[] graph, int[] parent, int par) {
// Idea is to mark a vertex by processing status
// 1. color = 0 -> If the vertex is not visited (white)
// 2. color = 1 -> To visit a vertex partially (gray)
// 3. color = 2 -> To visit a vertex completely (black)
// Already visited vertex.
if (color[node] == 2)
return;
// Cycle detected when a vertex is visited partially
if (color[node] == 1) {
cycleNumber++;
// Backtracking based on parents to find the complete cycle
int current = par;
visited[current] = cycleNumber;
while (current != node) {
current = parent[current];
visited[current] = cycleNumber;
}
return;
}
// Marking the parent of a vertex
parent[node] = par;
// Marking the node as partially visited
color[node] = 1;
// Running DFS on graph
for (Vertex child : graph[node].edges) {
// If the vertex is previously visited
if (child.id == parent[node])
continue;
// If the vertex is not visited
dfs(child.id, visited, color, graph, parent, node);
}
// Marking the vertex as completely visited
color[node] = 2;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int vertices = sc.nextInt();
int edges = sc.nextInt();
Vertex[] graph = new Vertex[vertices + 1];
// Stores the visited status of a vertex
int[] visited = new int[vertices + 1];
// Stores the processing status of a vertex
int[] color = new int[vertices + 1];
// Stores the parent of a vertex
int[] parent = new int[vertices + 1];
for (int i = 1; i <= vertices; i++) {
graph[i] = new Vertex(i);
graph[i].edges = new ArrayList<Vertex>();
}
Vertex v1, v2;
for (int i = 1; i <= edges; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
v1 = new Vertex(a);
v2 = new Vertex(b);
// Since it is an undirected graph, so we will update adjacency list of both nodes
graph[a].edges.add(v2);
graph[b].edges.add(v1);
}
int par = 0;
// Start making DFS call from 1st node in the graph
dfs(1, visited, color, graph, parent, par);
// Adjacency list to store the cycles
Map<Integer, ArrayList<Integer>> cycles = new HashMap<>();
for (int i = 1; i <= vertices; ++i) {
if (visited[i] != 0) {
cycles.computeIfAbsent(visited[i], k -> new ArrayList<>()).add(i);
}
}
// Printing the cycle
for (Map.Entry<Integer, ArrayList<Integer>> entry : cycles.entrySet()) {
int key = entry.getKey();
ArrayList<Integer> values = entry.getValue();
System.out.print("Cycle Number " + key + ": ");
for (int i : values) {
System.out.print(i + " ");
}
System.out.println();
}
sc.close();
}
}Time Complexity -
where is number of vertices and is the number of edges.
Space Complexity -
The auxillary space required will be where is the number of vertices.